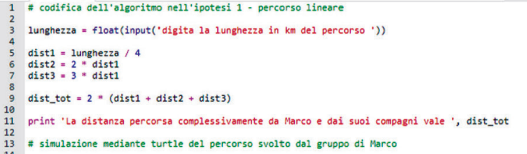
Un Esempio
SFIDA 6 La corsa campestre
Obiettivi Matematici
[ Partizioni di segmenti ]
Obiettivi Informatici
< Suddivisione in sottoproblemi,
Strutture di iterazione: i cicli for e while,
Uso di librerie />
Strumenti Applicativi
{ Python,
Libreria Turtle,
Trinket.io }
“ Sofia fa parte del comitato organizzatore della corsa campestre e con il suo gruppo deve posizionare lungo il percorso tre punti di ristoro,
equidistanti tra loro e dalla partenza e dall’arrivo. Per trasportare i gazebo e il materiale necessario per montare ogni punto di ristoro sono
necessari tutti i componenti del gruppo, pertanto, dopo aver completato l’installazione di un ristoro, tutti i ragazzi dovranno tornare alla
partenza per prendere il materiale per la nuova installazione.
Alla fine, Sofia e i suoi compagni, stanchi ma felici per il lavoro svolto, si chiedono quanta strada abbiano percorso in tutto.”
Si effettui nello storytelling l’operazione di comprensione, evidenziando la richiesta, e quella di astrazione
eliminando tutto ciò che risulta superfluo:
Sofia fa parte del comitato organizzatore della corsa campestre e con il suo gruppo deve posizionare lungo il percorso tre punti di ristoro,
equidistanti tra loro e dalla partenza e dall’arrivo. Per trasportare i gazebo e il materiale necessario per montare ogni punto di ristoro
sono necessari tutti i componenti del gruppo, pertanto, dopo aver completato l’installazione di un ristoro, tutti i ragazzi dovranno tornare
alla partenza per prendere il materiale per la nuova installazione.
Alla fine, Sofia e i suoi compagni, stanchi ma felici per il lavoro svolto, si chiedono quanta strada
abbiano percorso in tutto.
Nell’analisi di questa situazione vi sono alcuni elementi di cui tener conto:
- il problema va suddiviso in sottoproblemi:
- calcolare la distanza tra il primo ristoro e la partenza, che rappresenta anche, dal punto di vista geometrico, l’ampiezza di ciascuno dei sottointervalli in cui viene suddiviso l’intero intervallo Partenza/Arrivo
- calcolare la distanza di ciascuno dei tre ristori dalla partenza
- calcolare la lunghezza totale del percorso svolto dai ragazzi; ma tale sottoproblema prevede due ipotesi che possono avere i seguenti modelli:
- IPOTESI 1: il percorso si sviluppi in modo pseudo-lineare e il punto di arrivo non coincide con la partenza: può essere modellizzato tramite una retta
- IPOTESI 2: il percorso sia pseudo-circolare per cui partenza e arrivo coincidano:
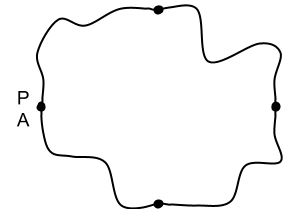
in questa seconda ipotesi, una volta installato il terzo ristoro, il ritorno al punto di partenza/arrivo sarà più breve
- il dato di input è implicito: non è stato espressamente indicato nel testo, ma per determinare la posizione dei punti di ristoro è evidentemente necessario conoscere la lunghezza del percorso
- si deve prestare particolare attenzione alla richiesta finale, che per essere soddisfatta necessita di determinare la distanza di ciascun punto di ristoro dalla partenza &hellip spesso gli studenti effettuano la lettura del testo del problema in modo superficiale e così non individuano l'algoritmo per risolvere la Sfida, ma che ne risolva una diversa. E anche se, come sosteneva Papert, un algoritmo che funziona è comunque corretto, in questo caso ha oviamente senso realizzare proprio quello che dia soluzione alla questione posta e non ad un’altra.

Considerati tutti questi aspetti ed effettuata la necessaria operazione di astrazione (si ricorda che non è fondamentale per la risoluzione del problema che si tratti della “Corsa di Primavera”), gli algoritmo risolutivo possono essere quindi così descritti:
IPOTESI 1 percorso pseudo-lineare
INPUT: lunghezza
ALGORITMO:
dist1 ← lunghezza / 4 1 ° sottoproblema
dist2 ← dist1 * 2 2° sottoproblema
dist3 ← dist1 * 3
dist_tot ← 2 * (dist1 + dist2 + dist3) 3° sottoproblema - riflettere sulla moltiplicazione per 2!
OUTPUT: dist_tot
IPOTESI 2 percorso pseudo-circolare
INPUT: lunghezza
ALGORITMO:
dist1 ← lunghezza / 4 1° sottoproblema
dist2 ← dist1 * 2 2° sottoproblema
dist3 ← dist1 * 3
dist_tot ← 2 * (dist1 + dist2) + lunghezza 3° sottoproblema - riflettere sull’espressione
OUTPUT: dist_tot
Nella pratica didattica quotidiana, accade spesso che gli alunni propongano di dividere la lunghezza del percorso per 3, visto che sono 3 i punti da collocare lungo il percorso!!! spiegazione ovviamente che deriva da un’analisi frettolosa e dalla mancata osservazione del modello rappresentato; se invece la modellizzazione fosse svolta in modo accurato essi si accorgerebbero che, come accade anche in geometria, 3 punti dividono in 4 parti un segmento. Questa modo superficiale di approcciarsi alla questione è certamente dovuto alla poca abitudine all’utilizzo di strumenti di modellizzazione a supporto dell’attività di ricerca della strategia risolutiva di una situazione problematica.
L'algoritmo presentato è solo uno dei molti possibili … vale la pena incitare gli studenti a proporne altri, soprattutto per quanto riguarda la soluzione del secondo sottoproblema. Infatti, altre possibili strategie per realizzare questo passo potrebbero essere:dist2 ← dist1 + dist1 e dist3 ← dist2 + dist1
dist2 ← lunghezza / 2 e dist3 ← lunghezza - dist1
Tutte strategie altrettanto valide!
Un approfondimento del problema riguarda poi la generalizzazione in merito al numero dei ristori. Infatti, se tale valore fosse un dato di input variabile non renderebbe più possibile utilizzare la struttura sequenziale dell'algoritmo che abbiamo precedentemente realizzato, poiché non sarebbe determinabile a priori il numero di variabili necessarie per contenere tutti i risultati intermedi necessari al calcolo finale. Ecco che gli studenti, spontaneamente se opportunamente accompagnati,individuano la necessità della struttura iterativa (ciclo) in modo da ripetere per un numero definito di volte la stessa sequenza di operazioni.
L’algoritmo che si presta meglio alla generalizzazione è il primo, cioè quello nell’ipotesi 1.
INPUT: lunghezza, num_ristori
ALGORITMO:
dist ← lunghezza/ (num_ristori+ 1) è opportuna una discussione per comprendere il significato del + 1 a denominatore
dist_tot ← 0
i ← 1
ripeti per num_ristori volte dapprima si sommano tutti i percorsi di andata dalla partenza a ciascun ristoro
dist_tot ← dist_tot + dist * i
i ← i + 1
dist_tot ← dist_tot * 2 si raddoppia la somma dato che i ritorni sono uguali alle andate
OUTPUT: dist_tot
In questo algoritmo può sembrare “strana” la scrittura
dist_tot ← dist_tot + dist * i
che va letta tenendo bene a mente il cencetto di assegnazione di un valore ad una variabile, e quindi nel modo seguente: sommare al contenuto della variabile dist_tot il contenuto della variabile dist moltiplicato per il contenuto di i e assegnare il risultato così trovato alla variabile dist_tot. Osservare bene che prima dell’inizio del ciclo alla variabile i, detta contatore, viene assegnato il valore 1 (operazione denominata inizializzazione), e ad ogni iterazione il contatore sarà incrementato, cioè gli verrà aggiunto 1, rendendo possibile ottenere le distanze dei ristori dalla partenza.
Le due istruzioni
dist_tot ← dist_tot + dist * i e i ← i + 1
vanno ripetuta ciclicamente tante volte quanti sono i ristori, accumulando nella variabile dist_tot, alla fine del ciclo, le distanze dei vari ristori dalla partenza; tale somma andrà poi raddoppiata per tener conto anche dei percorsi di ritorno al punto di partenza.
Il ciclo realizzato in questo algoritmo è il cosiddetto ciclo per enumerazione più conosciuto come ciclo for; tutti i linguaggi
di programmazione mettono a disposizione una specifica istruzione che racchiuda in sé tutti i passi necessari alla gestione del contatore:
identificare la variabile contatore, indicare il valore iniziale a cui deve essere inizializzato il contatore e il valore
finale che decreterà la fine del ciclo, specificare il passo di incremento del contatore. Quindi, al di là della sintassi specifica prevista da
ciascun linguaggio di programamzione, l’istruzione che realizza il ciclo for, ad esempio applicata al suddetto algoritmo, potrà essere
letta come segue: “per i che va da 1 fino a num_ristori esegui ...”.
Un classico esercizio da programmatori è simulare il ciclo for mediante un ciclo while, struttura di iterazione che sar&oarave; approfondita di seguito.
Si lascia ora al lettore la modifica di tale algoritmo per risolvere il problema nell’ipotesi 2 di percorso pseudo-circolare.
Questi algoritmi forniscono la soluzione di quella categoria di problemi in cui viene richiesto di dividere in parti uguali un elemento di
dimensione nota e possono quindi essere riutilizzati in tutte quelle situazioni.
Si propone di seguito una simulazione degli spostamenti effettuati da Sofia e dai suoi amici lungo il percorso della corsa mediante gli strumenti
della libreria Turtle di Python. Per semplicità si farà muovere il gruppo lungo un percorso perfettamente lineare.
Per scrivere codice col linguaggio Python ci sono varie possibilità e quelle che più frequentemente usate sono la shell e la
IDLE - Integrated DeveLopment Environment le quali mettono a disposizione un interprete a riga di comando e un ambiente di
edit per scrivere codice. Nel caso in cui si vogliano usare gli strumenti messi a disposizione dalla libreria Turtle, la gestione
delle diverse finestre nelle quali viene organizzato il codice e i risultati della sua esecuzione non è così immediata.
Si suggerisce quindi di utilizzare il portale web Trinket.io, un ambiente che permette di scrivere ed eseguire codice scritto in vari
linguaggi, mettendo a disposizione un ambiente unico di scrittura ed esecuzione.
Se ci si accontenta solo di scrivere ed eseguire codice, una volta messo a punto il programma sarà poi possibile provvedere al
suo salvataggio in locale sul nostro device mediante copia-incolla del testo in un file con estensione .py utilizzando un qualsiasi
editor, anche un semplice blocco note. Altrimenti, Trinket.io è anche un repository che consente anche di condividere il proprio
codice; in tal caso è però necessario effettuare la registrazione.